В мире треугольников

Оглавление Признаки равенства треугольников Виды треугольников Сумма углов треугольника Проверь себя!

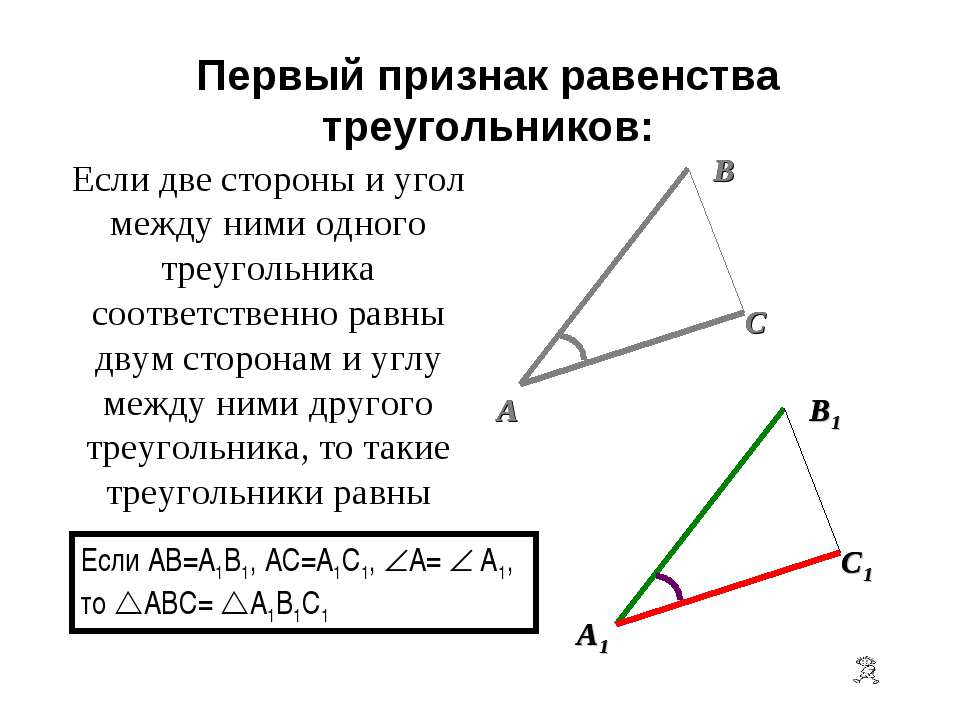
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны Если AB=A1B1, AC=A1C1, A= A1, то ABC= A1B1C1 Первый признак равенства треугольников:

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны Если AB=A1B1, A= A1, B= B1, то ABC= A1B1C1 Второй признак равенства треугольников: A1 B1 C1 B C A

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны B A C Если AB=A1B1, AC=A1C1, BC=B1C1 , то ABC= A1B1C1 Третий признак равенства треугольников B1 A1 C1

Виды треугольников

Свойство 1 В равнобедренном треугольнике углы при основании равны.

Свойство 2 Биссектриса, проведенная из вершины равнобедренного треугольника, является медианой и высотой.

Признаки равенства прямоугольных треугольников 1 признак. По двум катетам.

Признаки равенства прямоугольных треугольников 2 признак. По катету и гипотенузе.

Признаки равенства прямоугольных треугольников 3 признак. По катету и прилежащему острому углу.

Признаки равенства прямоугольных треугольников 4 признак. По гипотенузе и острому углу.

Сумма углов треугольника равна 180º

Внешний угол треугольника – это угол, смежный с внутренним углом треугольника ‹1-внешний угол.

Свойство внешнего угла треугольника. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. ‹3= ‹1+ ‹2

Проверь себя

Данные задания позволит вам проверить свои знания по темам: «Теорема о сумме углов треугольника» «Внешний угол треугольника. Теорема о внешнем угле треугольника» «Равнобедренный, прямоугольный треугольники и их свойства»

Желаем удачи!

1. 36 градусов 2. 40 градусов 3. 46 градусов

1. 50 градусов 2. 60 градусов 3. 55 градусов Молодец!

Умница! 1. 75 градусов 2. 65 градусов 3. 45 градусов

Молодец! 1. 45 градусов 2. 50 градусов 3. 135 градусов

Так держать! 1. 70 градусов 2. 60 градусов 3. 40 градусов

Ты просто умница! 1. 40 градусов 2. 35 градусов 3. 50 градусов

Хорошо! 1. 34 градуса 2. 37 градусов 3. 47 градусов

Отлично! 1. 100 градусов 2. 90 градусов 3. 110 градусов

Ты просто чудо! 1. 38 градусов 2. 42 градуса 3. 40 градусов

Ты просто гений! 1. 110 градусов 2. 130 градусов 3. 120 градусов

Еще чуть-чуть! 1. 115 градусов 2. 120 градусов 3. 130 градусов

Вот и финиш! 1. 120 градусов 2. 110 градусов 3. 60 градусов

поздравляем! Ты успешно справился с заданием.

А может подумаешь?