Третий признак подобия треугольников

Третий признак подобия треугольников

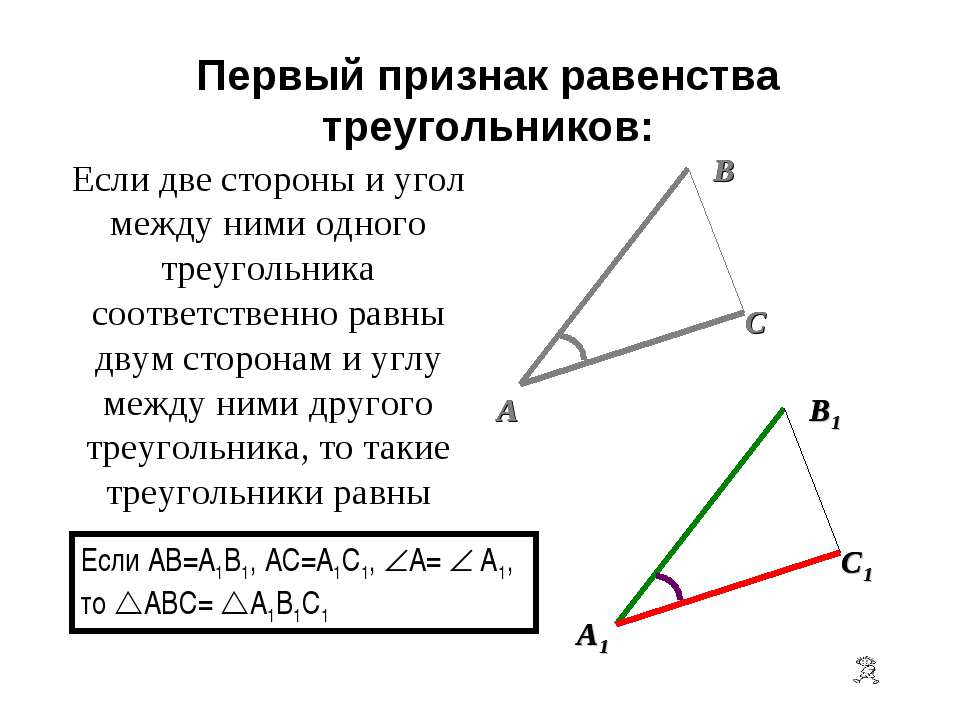
Вспомним подобные треугольники: Определение: треугольники называются подобными, если углы одного треугольника равны углам другого треугольника и стороны одного треугольника пропорциональны сходственным сторонам другого. Сходственными сторонами в подобных треугольниках называются стороны, лежащие против равных углов.

Теорема. Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны. Тогда по двум углам треугольники АВ1С и МРК подобны, значит,

Решение задачи В треугольнике АВС АВ = 4, ВС= 6, АС = 7. Точка Е лежит на стороне АВ. Внутри треугольника взята точка М так, что МВ = 5,25; МЕ = 4,5; АЕ = 1. Прямая ВМ пересекает АС в точке Р. Докажите, что треугольник АРВ – равнобедренный. Доказательство: ВЕ = АВ – АЕ = 4 – 1 = 3. Следовательно, треугольники АВС и ВЕМ подобны по трём сторонам, значит,

Михайлова Л. П. ГОУ ЦО № 173.