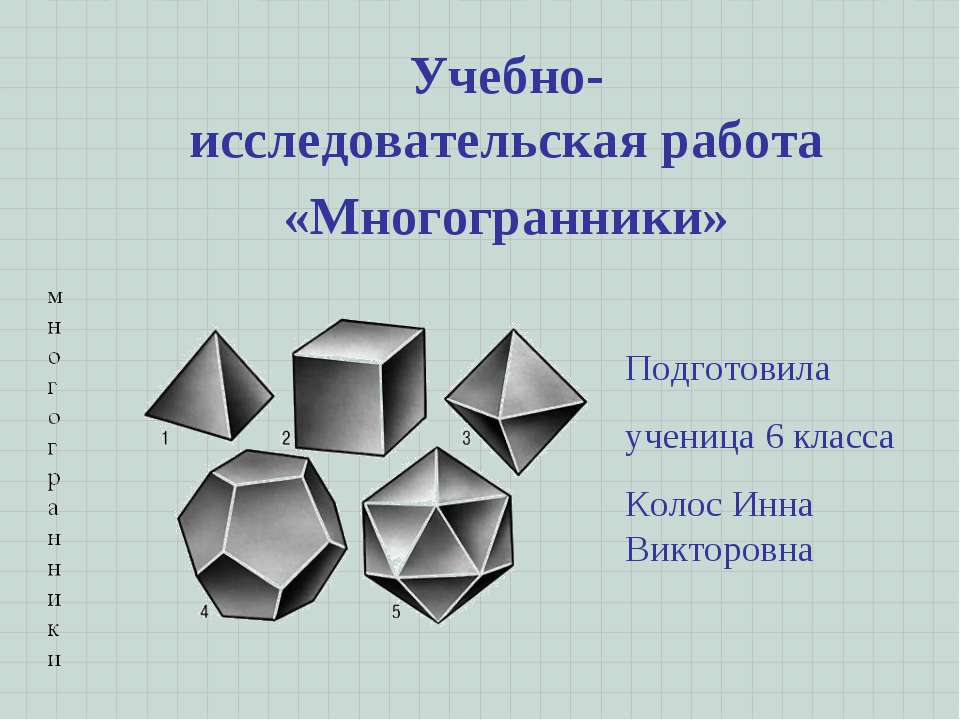
многогранники
- Рубрика: Презентации / Презентации по Математике
- Просмотров: 384
Презентация "многогранники" онлайн бесплатно на сайте электронных школьных учебников edulib.ru
Многогранник - геометрическое тело, ограниченное плоскими многоугольниками. Плоские многоугольники называются гранями многогранника стороны многоугольника – ребрами многогранника вершины многоугольника – вершинами многогранника. С
Пирамида называется правильной, если в основании лежит правильный многоугольник, а вершина проектируется в центр основания Пирамида - это многогранник Основанием является многоугольник боковые грани – треугольники (n-угольная пирамида имеет n+1 граней)
Правильная призма она прямая основание ее правильный многоугольник. ПРИЗМА – это многогранник основания равные многоугольники боковые грани параллелограммы четырехугольная призма в основании лежит четырехугольник треугольная призма в основании лежит треугольник Прямая призма боковые ребра перпендикулярны основаниям
Параллелепипед – это призма Свойства параллелепипеда: 1. Противоположные грани параллелепипеда параллельны и равны. 2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам. основанием которой является параллелограмм Параллелепипед, основанием которого является прямоугольник или квадрат называется прямым
Тетраэдр ( от ,,тетра”- четыре и греческого ,,hedra” - грань) состоит из 4-х правильных треугольников, в каждой его вершине сходятся 3 ребра. тетраэдр-огонь Тетраэдр символизировал огонь, т.к. его вершина устремлена вверх
Гексаэдр (куб) гексаэдр (куб) - земля Гексаэдр (куб) символизировал землю, так как самый «устойчивый» ( от греческого ,,гекса” - шесть и ,,hedra” - грань) имеет 6 квадратных граней, в каждой его вершине сходятся 3 ребра. Гексаэдр больше известен как куб (от латинского ,,cubus”; от греческого ,,kubos”.
Октаэдр октаэдр-воздух (от греческого okto - восемь и hedra - грань) имеет 8 граней (треугольных), в каждой вершине сходятся 4 ребра. Октаэдр символизировал воздух, как самый "воздушный"
Икосаэдр икосаэдр-вода Икосаэдр символизировал воду, так как он самый «обтекаемый» (от греческого eikosi - двадцать и hedra - грань) имеет 20 граней (треугольных), в каждой вершине сходится 5 рёбер
Додекаэдр додекаэдр-вселенная Додекаэдр воплощал в себе "все сущее", символизировал все мироздание, считался главным (от греческого dodeka - двенадцать и hedra - грань) имеет 12 граней (пятиугольных), в каждой вершине сходятся 3 ребра.
Заполни таблицу 4 4 6 6 6 8 8 12 12 12 12 20 20 30 30 Название Тетраэдр Куб Октаэдр Додекаэдр Икосаэдр Форма граней Число граней Число ребер Число вершин
Теорема Эйлера: Число вершин - число ребер + число граней =2 Швейцарский, немецкий и российский математик автор более чем 800 работ по математическому анализу, дифференциальной геометрии, теории музыки и др. Леонард Эйлер (1707-1783) Число вершин, рёбер и граней правильных многогранников связано друг с другом интересным соотношением.
Великая пирамида в Гизе Александрийский маяк Многогранники в архитектуре. Никольский собор Галикарнасский мавзолей Башня Сююмбике Мечеть Кул-Шариф
http://www.yandex.ru/ (картинки, анимашки) http://ru.wikipedia.org/ http://otherreferats.allbest.ru/mathematics/00050000_0.html Библиография