Как измерить расстояние между родственниками

Муниципальное бюджетное общеобразовательное учреждение “Кабановская СОШ” “Как измерить расстояние между родственниками” Автор: Ученица 5“б” класса Балабойко Анастасия Вячеславовна Руководитель: Учитель математики Жукова Валентина Витальевна

Графом называют множество, в котором некоторые пары элементов выделены; элементы каждой выделенной пары называют смежными друг другу или просто смежными. Пример – множество станций метро какого-то города. Будем считать станции смежными, если между ними нет промежуточных станций. На изображенной на рисунке части схемы линий московского метро станции «Динамо» и «Аэропорт» смежные, а «Динамо» и «Сокол» несмежные. Очень удобно изображать элементы графа точками (или, скажем, кружочками) на плоскости, причем смежные элементы соединять линией, например отрезком. При таком изображении элементы графа принято называть вершинами, а линии, соединяющие смежные вершины, - ребрами. Например, в графе на этом рисунке пять вершин и четыре ребра. Граф

Любой многоугольник можно считать графом. У треугольника любые две вершины смежные, а у четырехугольника четыре пары смежных вершин и две пары несмежных. Если в четырехугольнике провести диагонали, то получится граф, у которого любые две вершины смежные.

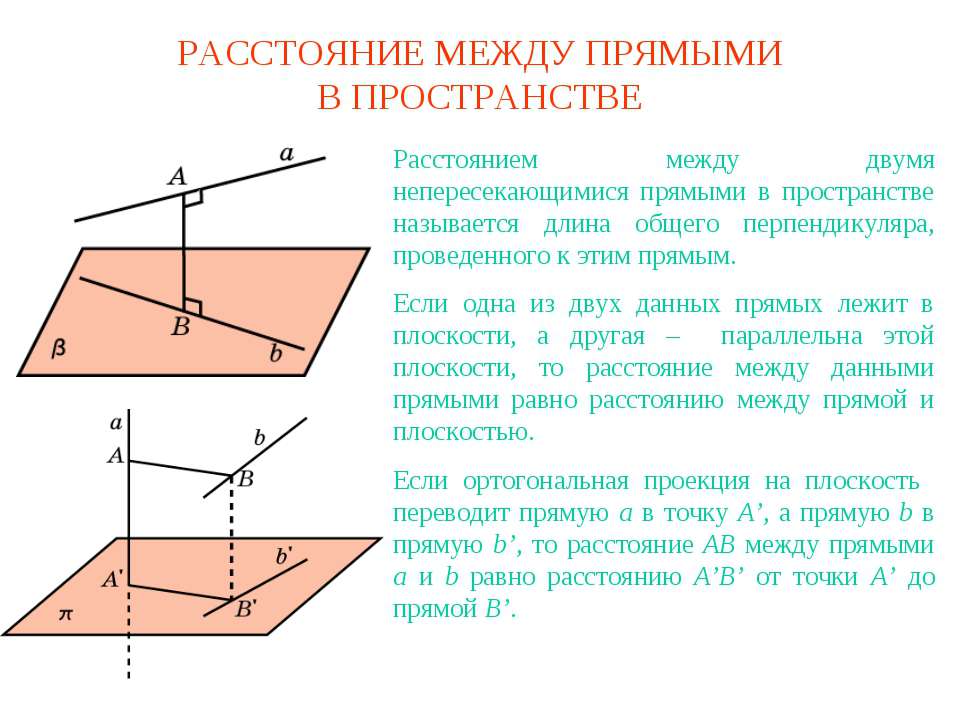
При изображении графа на плоскости неважно, каково обычное расстояние между вершинами и какой вид имеют ребра. Графы на трех приведенных ниже рисунках считаются одинаковыми. Графы на плоскости. В каждом из них 3 вершины и 2 ребра, причем в каждом графе вершины А и В, В и С смежны, а А и С не смежны. Именно таким описанием вершин и ребер можно задать указанный один и тот же граф.

О путях и графах. Если дан граф, то двигаясь по его ребрам (как «по дорогам»), можно попадать из одной вершины в какую-нибудь другую. Всякую цепочку ребер, соединяющую две вершины, называют путем между этими вершинами, а число ребер в пути – длиной этого пути. Обозначать путь удобно цепочкой вершин, последовательно участвующих в этом пути. Например, из вершины А в вершину F можно пройти по пути ACF, или по пути ADEF, или по пути ACDEF.

Граф родственных отношений. Семья, в которой есть отец, мать, их сын и дочь, а также мать отца, изображается следующим графом: Рассматривая пути между его вершинами, мы видим, что расстояние между бабушкой и внучкой равно 2, между братом и сестрой тоже равно 2.

С помощью графов можно составить генеалогическое древо своей семьи.

Задача о Кенигсбергских мостах. В городе Кенигсберге (ныне Калининград – самый западный областной центр России) есть остров, окруженный рекой, через которую перекинуто семь мостов. Можно ли обойти их все, пройдя только однажды через каждый мост? Кенигсбергские обыватели истоптали много обуви, пытаясь обойти мосты так, как требует условие, но безуспешно. В 1736 году о «непроходимых» Кенигсбергских мостах прослышали в Петербурге, где занятной задачей заинтересовался сам Леонард Эйлер (математик из Швейцарии с 1727 г. работал в Российской Академии наук). Он быстро понял причину затруднений, причем для этого ему не понадобилось ехать в Кенигсберг. Вместо плана Кенигсберга можно рассматривать просто граф, в котором ребра соответствуют мостам, а вершины – различным частям города.

Задача о мостах превращается в такую задачу про этот граф: есть ли в графе путь, который проходит по разу через каждое ребро? Допустим, что, идя по такому пути, мы зашли по какому-то ребру a в вершину А. Понятно, что выйти из А придется по другому ребру (скажем, b) – ведь проходить второй раз через ребро a не разрешается. Итак, к вершине А ведут по крайней мере 2 ребра: a и b. Если, продолжая движение, мы снова попадем в вершину А по еще одному ребру с, то выйдем из А по опять-таки новому, «нехоженому» ребру d, т.е. возникнет еще одна пара ребер. И так далее – ребра, сходящиеся в вершине А, разбиваются на такие пары: Задача о Кенигсбергских мостах. Итак, вывод: раз ребра, сходящиеся в вершине А, можно разбить на пары, то таких ребер четное число. Значит, если в каком-либо графе есть путь, который проходит ровно по одному разу через каждое ребро, то в каждой вершине такого графа, кроме, может быть, двух, должно сходиться четное число ребер. Ребро, по которому мы зашли в А в первый раз Ребро, по которому мы покинули А в первый раз Ребро, по которому мы зашли в А во второй раз Ребро, по которому мы покинули А во второй раз Ребро, по которому мы зашли в А в третий раз Ребро, по которому мы покинули А в третий раз … …

Сделав вывод, посмотрим снова на граф. В каждой его вершине сходится нечетное число ребер. Значит, через ребра этого графа нельзя пройти так, чтобы на каждом ребре побывать лишь однажды. Вот поэтому и не удавалось обойти Кенигсбергские мосты. Выводы Работа Эйлера, в которой была решена задача о Кенигсбергских мостах, была напечатана в том же, 1736 году в «Записках» Петербургской академии наук. Его работа ознаменовала зарождение нового раздела математики – теории графов. Это была самая первая, но далеко не последняя область современной математики, местом рождения которой стала наша страна.