Презентация "III признак равенства треугольников"

Классная работа
Третий признак равенства треугольников
Стр. 38

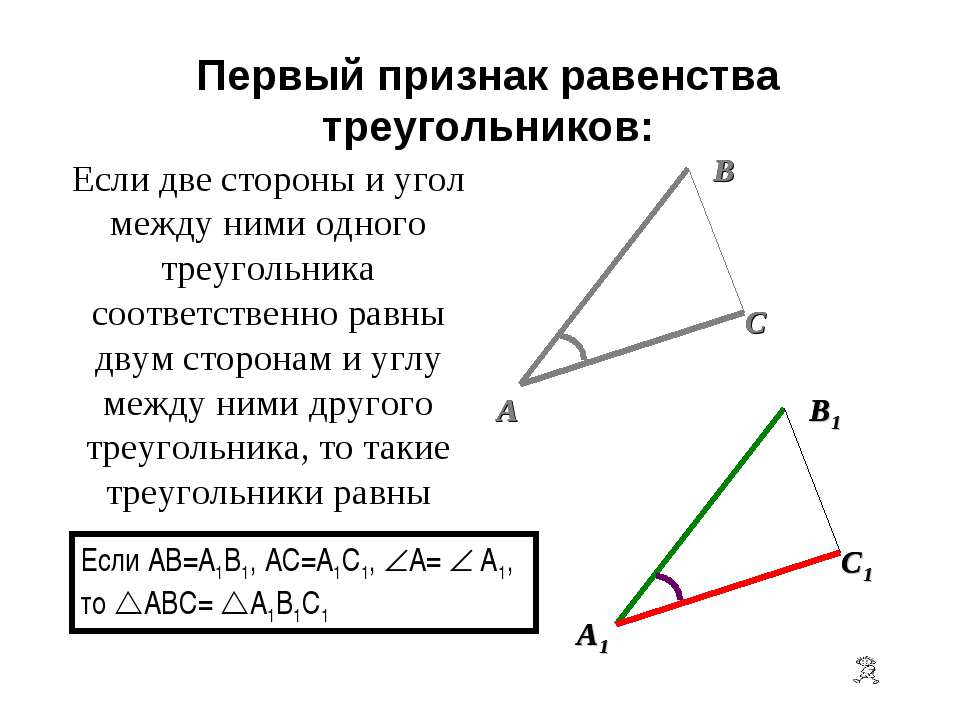
Первый признак равенства треугольников
Теорема : Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
𝑨 𝟏
𝑩 𝟏
𝑪 𝟏
𝑨
𝑩
𝑪
Стр. 29

Второй признак равенства треугольников
Теорема : Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
𝑨 𝟏
𝑩 𝟏
𝑪 𝟏
𝑨
𝑩
𝑪
Стр. 37

Третий признак равенства треугольников
Теорема : Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
𝑨 𝟏
𝑩 𝟏
𝑪 𝟏
𝑨
𝑩
𝑪
Стр. 38

𝑨 𝟏
𝑩 𝟏
𝑪 𝟏
𝑨
𝑩
𝑪
Дано: 𝐴𝐵= 𝐴 1 𝐵 1 , 𝐴𝐶= 𝐴 1 𝐶 1 , 𝐶𝐵= 𝐶 1 𝐵 1
Доказать: ∆𝐴𝐵𝐶=∆ 𝐴 1 𝐵 1 𝐶 1
Доказательство: приложим ∆𝐴𝐵𝐶 к ∆ 𝐴 1 𝐵 1 𝐶 1 так, чтобы совместились вершины 𝐴𝐵 и 𝐴 1 𝐵 1 соответственно. Вершины 𝐶 и 𝐶 1 по разные стороны от прямой 𝐴 1 𝐵 1 .
𝑨 𝟏 (𝑨)
𝑩 𝟏 (𝑩)
𝑪
𝑪 𝟏

𝑨 𝟏 (𝑨)
𝑩 𝟏 (𝑩)
𝑪
𝑪 𝟏
Т.к. 𝐴𝐶= 𝐴 1 𝐶 1 , 𝐶𝐵= 𝐶 1 𝐵 1 , то ∆𝐶 𝐵 1 𝐶 1 и ∆С 𝐴 1 𝐶 1 − равнобедренные ⇒
⦟1=⦟2, ⦟3=⦟4 ⇒ ⦟ 𝐴 1 𝐶 𝐵 1 =⦟ 𝐴 1 𝐶 1 𝐵 1 .
1
2
3
4
𝐴𝐶= 𝐴 1 𝐶 1 , 𝐶𝐵= 𝐶 1 𝐵 1 , ⦟𝐶=⦟ 𝐶 1 ⇒ ∆𝐴𝐵𝐶=∆ 𝐴 1 𝐵 1 𝐶 1 по первому признаку равенства треугольников.

Дано: AB=CD, BC=AD
Доказать: ⦟1=⦟2
Решение:
В ∆АВС и ∆ACD
AB=CD, BC=AD, АС – общая сторона ⇒ ∆АВС=∆ACD по третьему признаку.
⦟1=⦟2 , т.к. против равных сторон лежат равные углы.
Ответ: ⦟1=⦟2


1
2
𝑪
𝑫
𝑩
𝑨

Дано: АВ=ВС, АК=КС, ⦟АКЕ=⦟РКС
Доказать: ∆АКЕ=∆КРС
Решение:
АВ=ВС ⇒ ∆АВС – равнобедренный ⇒ ⦟ВАС=⦟ВСА, как углы при основании.



𝑨
𝑩
𝑪
𝑲
𝑬
𝑷
АК=КС, ⦟АКЕ=⦟РКС по условию ⇒ ∆АКЕ=∆КРС по второму признаку равенства треугольников.
Ответ: ∆АКЕ=∆КРС

№ 125, 127, 130,
Стр. 40 – 41.
Решить номера:

№ 129, 131, стр. 41
Выучить теорему
Домашняя работа: